All You Need To Know About The Breadth First Search Algorithm

All You Need To Know About The Breadth First Search Algorithm

• 

  Pradyumn Singh / 2 Months
• 0
• 5 min read

• Developer Job Interview
• Front-End Developer
• Front-End Developer Interview
• Interview Questions

Introduction

When it comes to exploring or traversing data structures like graphs or trees, the Breadth First Search (BFS) algorithm stands out as one of the most fundamental and widely used techniques. If you’re diving into the fascinating world of algorithms, understanding BFS is a must! In this blog, we’ll break down BFS in a simple, approachable way that includes examples, illustrations, and code snippets. By the end, you’ll see why it’s a cornerstone in computer science, especially in AI and data engineering.

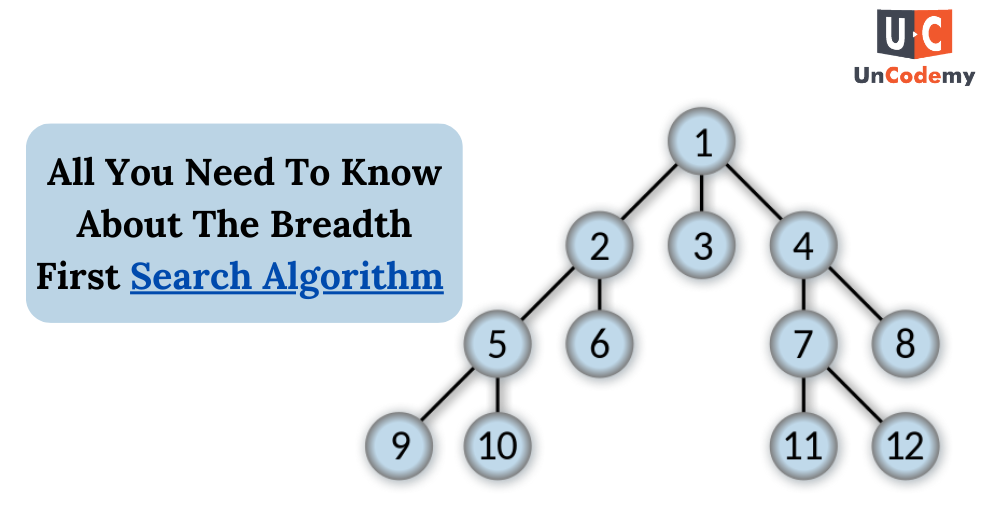
What Is the Breadth First Search Algorithm?

• The Breadth First Search (BFS) algorithm is a graph traversal technique that explores all nodes at the current depth level before moving to the next level. It’s like ripples from a stone thrown into a pond—spreading outwards level by level.

Key Features of BFS:

• Explores nodes level by level.
• Uses a queue data structure to track nodes to visit.
• Guarantees the shortest path in an unweighted graph.
• Widely used in AI for problem-solving, such as in games and pathfinding.

BFS Algorithm: Step-by-Step

• Initialize: Start from a source node, mark it as visited, and enqueue it.
• Dequeue and Explore: Remove the front node from the queue and examine its neighbors.
• Enqueue Unvisited Neighbors: Add all unvisited neighbors to the queue and mark them as visited.
• Repeat: Continue until the queue is empty.

BFS Example

Graph:

A
/ \
B   C
|   |
D   E

Starting from node A, the BFS traversal order is: A → B → C → D → E

Python Code Example

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node, end=" ")
            visited.add(node)
            queue.extend(neighbor for neighbor in graph[node] if neighbor not in visited)

# Graph represented as an adjacency list
graph = {
    'A': ['B', 'C'],
    'B': ['D'],
    'C': ['E'],
    'D': [],
    'E': []
}

bfs(graph, 'A')

Output: A B C D E

BFS vs. DFS

• BFS (Breadth First Search): Explores level by level using a queue.
• DFS (Depth First Search): Explores as far as possible along each branch using a stack (or recursion).
• BFS guarantees the shortest path in unweighted graphs, while DFS may go deep without finding the shortest route.
• BFS uses more memory due to storing nodes at each level, DFS uses less but may get stuck in deep or infinite branches if not handled correctly.

BFS Algorithm in AI

• Pathfinding in games (e.g., finding the shortest route for a character).
• Solving puzzles like the Rubik’s Cube.
• Searching in social networks (e.g., finding the shortest connection between two users).

BFS and DFS Algorithm With Example

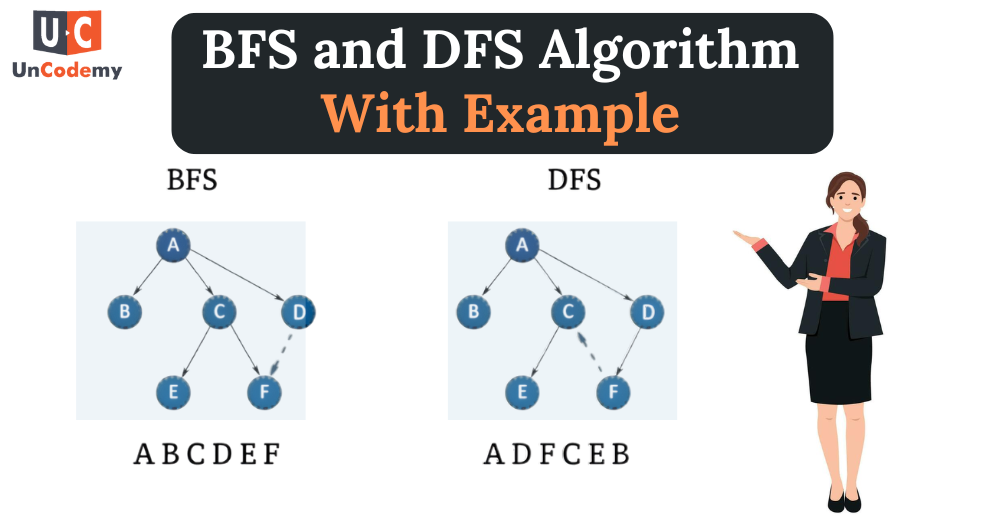
Consider a maze-solving robot. BFS ensures the robot finds the shortest path to the exit, while DFS might explore all possible routes, which can be inefficient in larger mazes.

BFS in Action: Solving a Maze

Imagine a maze as a graph where cells are nodes, and edges connect adjacent cells. BFS explores all cells layer by layer, ensuring it finds the shortest path to the exit.

Visualization of BFS

Graph Initialization:
A
/ \
B   C
|   |
D   E

• Start with A in the queue.
• Dequeue A, enqueue B and C.
• Dequeue B, enqueue D.
• Dequeue C, enqueue E.
• Continue until the queue is empty.

Common Applications of BFS

• Web Crawling: BFS is used to traverse web pages and index them systematically.
• Social Networks: To find degrees of separation between users.
• Network Broadcasting: Helps send messages to all nodes in a network.
• AI Pathfinding: Ideal for shortest path algorithms in games and robotics.

Advantages of BFS

• Guarantees the shortest path in unweighted graphs.
• Simple and easy to implement.
• Great for problems requiring layer-wise exploration.

Limitations of BFS

• Requires more memory compared to DFS.
• Can be slower on large graphs due to visiting all neighbors at each level.

BFS Algorithm Example: Solving a Problem

Problem: Find the shortest path from A to E in the following graph:

A
/ \
B   C
|   |
D   E

Solution: Using BFS, the shortest path is: A → C → E

“Simplicity is the soul of efficiency.” — Austin Freeman
BFS exemplifies this idea by offering a straightforward, efficient way to explore graphs.

Conclusion

The Breadth First Search algorithm is a powerful tool in the realm of computer science and AI. Its simplicity, coupled with its ability to guarantee the shortest path in unweighted graphs, makes it a go-to choice for numerous applications. By mastering BFS, you're not just learning an algorithm; you're opening doors to solving complex problems, one level at a time.