If you want to create apps that run well, knowing your advanced data structures is a must. One of the best tree structures you can learn is the red-black tree. It's a self-balancing binary search tree that keeps things running smoothly using some color codes and rotations. This guide will check out red-black trees, how you can use them, and why programmers should learn about them.
Okay, so a red-black tree is like a special kind of binary search tree. Each spot in the tree is either red or black, and it has rules to keep things balanced all the time. Regular binary search trees can get messed up and slow down quite a bit, but red-black trees always stay pretty speedy for adding, removing, or finding stuff.
What's cool is that red-black trees can fix themselves to stay balanced using colors and rotations. When you add or remove spots, the tree rearranges itself to stay balanced. The longest route from top to bottom is never more than double the shortest route. This makes red-black trees really dependable when you need things to work fast all the time.
Folks studying computers often learn about red-black trees as something a bit more advanced, after they have the basics down. These lessons give you both the knowledge and how to use these balanced trees.
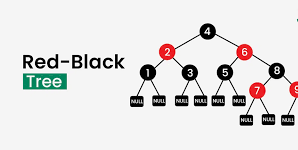
Okay, so red-black trees stay balanced because they follow five basic rules. Knowing these rules is key to using them right.
First off, each node is either red or black. This color thing is how the tree keeps its shape by checking and changing colors easily.
Next, the very top node is always black. This makes things easier to start with and simplifies stuff by avoiding weird exceptions.
Also, the empty leaf nodes are seen as black. So, every path from the top to a leaf has at least one black node, which helps keep the tree balanced.
Then, if a node is red, its kids have to be black. This stops red nodes from being next to each other, which messes with the balance and slows things down.
Finally, every route from any node down to the leaves has the same number of black nodes. This is called the black height. It makes sure the tree stays balanced, giving you that log thing that makes red-black trees worth using.
Red-black trees stay balanced by spotting and fixing issues with rotations and color swaps. Adding or removing stuff might break the tree's rules for a bit, kicking off a fix.
Rotations are key to keeping things balanced in red-black trees. Left and right rotations help the tree rearrange itself while keeping its search-tree setup. These tweaks are quick and only mess with a small part of the tree, so they're fast and reliable.
Color changes team up with rotations to get the red-black tree rules back in order. If rotations can't do it alone, the algorithm changes node colors to fit what's needed. This mix of structure and color changes means the tree can handle any adding or removing without losing its balance.
The fix-up in red-black trees always wraps up in a set amount of steps. Because it’s easy to guess, red-black trees are good for things that need solid performance, like real-time apps.
Putting new items into a red-black tree is trickier than just adding them to a regular binary search tree. But this difficulty is worth it because you get way better performance and can really count on it. The process of inserting starts like any normal binary search tree. After that, there's a fixing stage, which puts the red-black tree properties back in place.
When you add a new item, it starts out red. This is to keep the tree's rules from being broken. Red items usually don't mess up the black height rule, so it's safer to start with them as red.
Once the red item is in, the tree checks to see if any rules were broken. If the new item’s parent is also red, then there’s a problem that needs fixing with turns and color swaps. How it gets fixed depends on the colors and spots of the item’s relatives.
The fixing-after-inserting stage looks at a few situations based on how things are set up around the new item. Each situation has its own set of turns and color changes that fix the tree while keeping the binary search tree in order. Students in programs ( like Uncodemy’s data structure courses in Noida) learn about these situations with examples and practice exercises.
Taking stuff out of a red-black tree is usually trickier than putting it in. That's because when you delete something, it can really mess with how the tree is set up. You have to make sure it still works like a binary search tree but also keeps its red-black color rules.
If you're getting rid of a node that has two kids, the usual thing to do is swap it with the one before or after it in order, and then delete *that* one. That makes it easier because you're only deleting a node with one kid (at most), which makes fixing things up easier.
Things get complicated when you delete black nodes because that can screw up the black height rule. Deleting a red node is chill, usually, because it doesn't change the black height on any path through the tree.
When rebalancing after a deletion, there are a bunch of specific situations, and what you do depends on the color and shape of the deleted node's family. These situations might involve twisting parts of the tree around (rotations), swapping colors, and sometimes running the deletion steps again. You gotta examine these situations and practice them carefully. That's why upper-level data structure classes teach deletion operations thoroughly.
Red-black trees are fast because they keep themselves fairly balanced. The tree's height is never more than roughly 2*log(n+1), so almost every action takes O(log n) time. This is true even if you have millions of pieces of data.
Searching a red-black tree is just like searching a regular binary tree. You start at the top and keep going down the right path. The good thing is that because the tree is balanced, you'll never have to check every piece of data one by one.
Putting things in or taking them out takes a bit longer than with simple trees because the tree needs to fix itself to stay balanced. But it’s still O(log n) in the long run. This is a good deal if you don't know what your data will look like.
Red-black trees don't use much extra memory. Every item in the tree needs a tiny bit more room to mark its color (red or black), that's all. So, they are good if you want speed and don't have a ton of memory to spare.
Red-black trees? They're all over the place—system stuff, databases, data structures. They're good because they're reliable, don't hog memory, and you know what you're getting. That's why they're great where things need to be predictable.
A lot of standard libraries use them for things like associative containers. For example, C++ often uses red-black trees for its map and set containers, giving programmers a way to store and grab key-value pairs easily.
OS kernels? Yep, red-black trees are there too, for things like scheduling processes, dealing with memory, and managing files. Because they perform consistently, they're great for systems where timing is critical.
Databases also use them for indexing and making searches faster. The way these trees stay balanced means database queries run smoothly, no matter how the data is arranged or added.
When students learn about this stuff in data structure courses, they see how the theories turn into real solutions that keep computers running.
Red-black trees are a great example of smart algorithm design. They mix math with real-world use in a way that's rare for data structures. The way they keep themselves balanced using colors and rotations shows how computer science ideas turn into strong tools.
Learning red-black trees takes time and practice, and you need to get the main ideas. Everything about them, like how colors work and how they rebalance, helps them work well and be dependable.
As you learn more about data structures, keep in mind that red-black trees are a good starting point for understanding other balanced trees and self-organizing systems. What you learn from red-black trees can be used in many areas of computer science and software development.
If you're working on system software, database systems, or fast apps, knowing how red-black trees work can help you create data structures that are efficient and reliable. Putting in the time to understand these trees is worth it for your career as a programmer.
Students who study computer science in places like Uncodemy's data structure courses get the organized learning and expert help they need to learn these tricky subjects. Mixing what you learn with hands-on practice is a strong base for solving tough coding problems.
What's the main advantage of red black trees over regular binary search trees?
Red black trees maintain automatic balance through color properties and rotations, guaranteeing O(log n) performance for all operations, while regular binary search trees can degrade to O(n) performance in worst-case scenarios.
How do red black trees compare to AVL trees in terms of performance?
AVL trees maintain stricter balance and offer slightly better search performance, but red black trees have faster insertion and deletion operations due to fewer rebalancing requirements, making them better for modification-heavy applications.
Why are red black trees used in many standard library implementations?
Their combination of guaranteed logarithmic performance, minimal memory overhead (one bit per node), and relatively simple implementation compared to other balanced trees makes them ideal for general-purpose associative containers.
What happens if I violate the red black tree properties during implementation?
Violating the properties can lead to unbalanced trees with degraded performance or infinite loops in rebalancing algorithms. Proper implementation requires careful handling of all rebalancing cases and thorough testing.
Can red black trees handle duplicate keys effectively?
Standard red black trees don't handle duplicates directly, but you can modify them to allow duplicates by adjusting the insertion rules or storing multiple values per node, depending on your application requirements.
How difficult is it to implement a red black tree from scratch?
Implementation requires a solid understanding of tree algorithms and careful attention to the complex rebalancing cases. While challenging, it's achievable with proper study and systematic testing of all edge cases.
Personalized learning paths with interactive materials and progress tracking for optimal learning experience.
Explore LMSCreate professional, ATS-optimized resumes tailored for tech roles with intelligent suggestions.
Build ResumeDetailed analysis of how your resume performs in Applicant Tracking Systems with actionable insights.
Check ResumeAI analyzes your code for efficiency, best practices, and bugs with instant feedback.
Try Code ReviewPractice coding in 20+ languages with our cloud-based compiler that works on any device.
Start Coding
TRENDING
BESTSELLER
BESTSELLER
TRENDING
HOT
BESTSELLER
HOT
BESTSELLER
BESTSELLER
HOT
POPULAR